Chi-Square Test of Independence

1. Introduction

The Chi-Square Test of Independence is a vital statistical test for examining whether two categorical variables are independent. It helps researchers determine whether the distribution of one variable differs depending on the categories of another. This test is widely used in various fields, from social sciences to marketing and healthcare, to explore relationships between two categorical variables.

In this blog post, we will explain what the Chi-Square Test of Independence is, how to perform it in SPSS, and how to interpret its results. We will guide you through the steps of conducting this test, ensuring that you can confidently apply it to your own data analysis.

2. What is the Chi-Square Test of Independence in Statistics?

The Chi-Square Test of Independence is a non-parametric statistical test used to examine whether two categorical variables are independent of each other. This means it checks if the occurrence of one variable affects the distribution of the other. It compares observed frequencies in a contingency table to the expected frequencies if there were no association between the variables.

Several key terms relate to the Chi-Square Test of Independence:

• Cross Tabulation: A method of summarising categorical data by displaying the frequency distribution of the variables in a matrix format.
• Contingency Table: A table used in the Chi-Square test that shows the observed frequency counts for each combination of the variables.
• Effect Sizes for Chi-Square: Effect size measures include Phi (φ), Cramér’s V, Gamma, Somers’d, and Kendall’s tau-b. These effect sizes help quantify the strength of the association.

Effect Size Chi-square Test

• Phi (φ): Phi is used when both variables in the contingency table are dichotomous (2×2 table). It measures the degree of association between two binary variables, with values ranging from -1 to +1, where values closer to ±1 indicate a stronger association.
• Cramér’s V: Cramér’s V is a generalisation of Phi and is used when the contingency table is larger than 2×2. It adjusts Phi for the size of the table and also ranges from 0 to 1, with values closer to 1 indicating a stronger association.
• Gamma: Gamma measures the strength and direction of association between two ordinal variables. It ranges from -1 to +1, where positive values indicate a positive relationship and negative values indicate an inverse relationship.
• Somers’ d: Somers’ d is an asymmetrical measure used when one variable is considered dependent. It measures the strength and direction of association between two ordinal variables, and like Gamma, it ranges from -1 to +1.
• Kendall’s tau-b: This measure is used for square contingency tables where both variables are ordinal. It adjusts for ties in the data and provides an indication of the strength and direction of the relationship between the two variables.
• Kendall’s tau-c: Similar to tau-b but used for non-square tables, tau-c adjusts for different numbers of categories in each variable.

3. What is the Formula for the Chi-Square Test?

The formula for the Chi-Square Test of Independence is:

χ2=∑(O−E)2E\chi^2 = \sum \frac{(O – E)^2}{E}χ2=∑E(O−E)2​

Where:

• O represents the observed frequency for each category.
• E represents the expected frequency for each category, assuming no association between the variables.

This formula calculates the squared differences between observed and expected frequencies, divided by the expected frequencies. Summing these values across all cells gives the Chi-Square statistic, which is compared to a critical value from the Chi-Square distribution to determine statistical significance.

4. What is the Chi-Square Test of Independence used for?

The Chi-Square Test of Independence is primarily used to determine if there is a statistically significant association between two categorical variables. Researchers in fields like social sciences, healthcare, and marketing use this test to investigate relationships between variables like age and voting behaviour, or gender and customer preferences.

By identifying whether two variables are independent, this test can help guide decision-making and strategy. For example, marketers might want to know if product preference differs by age group, or healthcare professionals might explore whether the incidence of a disease varies across genders. The results of the test can reveal important patterns and associations that inform future research or actions.

5. Explain Differences among Chi-Square Tests of Independence, Goodness Fit, Association, Homogeneity and Fisher’s Exact Test

• Chi-Square Test for Association: Determines if two categorical variables are associated or independent by comparing observed and expected frequencies in a contingency table.
• Chi-Square Test of Independence: Similar to the test for association, it assesses whether two variables are independent. The key difference lies in the context of the research question, with independence tests often focusing on whether the distribution of one variable is unaffected by the other.
• Chi-Square Goodness-of-Fit Test: Compares observed frequencies of a single categorical variable to a theoretically expected distribution. Researchers use it to determine if a sample fits a specific distribution.
• Chi-Square Test of Homogeneity: Tests whether two or more groups are homogeneous in terms of the distribution of a categorical variable. This test is used to compare the proportions across different populations.
• Fisher’s Exact Test: Fisher’s Exact Test is an alternative to the Chi-Square test for 2×2 contingency tables, especially when sample sizes are small or when expected frequencies are less than 5. Unlike the Chi-Square test, Fisher’s Exact Test provides an exact p-value, making it more accurate when dealing with small or sparse data. It is particularly useful when the assumptions of the Chi-Square test are not met.

6. What are the Assumptions of the Chi-Square Test?

Before performing the Chi-Square Test of Independence, researchers must ensure that certain assumptions are sufficient.So, Failing to meet these assumptions may lead to inaccurate results, so it is essential to understand and verify them before proceeding with the analysis.

• The variables must be categorical.
• The observations must be independent of one another.
• The expected frequency in each cell of the contingency table should be 5 or greater.
• The sample size should be sufficiently large to ensure reliable results.
• The data should not contain overlapping categories.

7. What is the Hypothesis of the Chi-Square Test of Independence?

The hypotheses for the Chi-Square Test of Independence are:

• Null Hypothesis (H₀): The two categorical variables are independent. This means that the distribution of one variable is not affected by the other.
• Alternative Hypothesis (H₁): The two categorical variables are not independent, meaning the distribution of one variable differs depending on the other.

Rejecting the null hypothesis suggests that there is a significant relationship between the two variables, indicating they are not independent of one another.

8. An Example of the Chi-Square Test of Independence

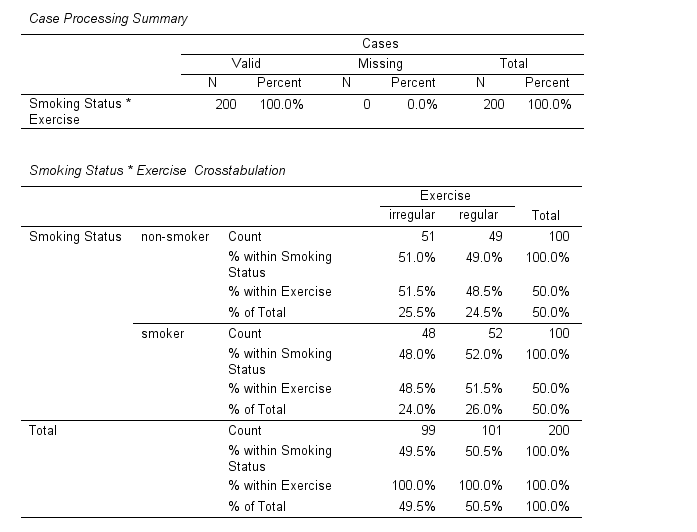
Imagine a study that investigates whether there is a relationship between smoking status (smoker or non-smoker) and exercise frequency (regular or irregular). The two categorical variables in this case are smoking status and exercise frequency.

In this example, a researcher collects data from 200 individuals and records whether each person smokes and how often they exercise. After organising the data into a contingency table, the researcher performs the Chi-Square Test of Independence in SPSS to see if the proportion of smokers and non-smokers differs between regular and irregular exercisers.

Step by Step: Running Chi-Square Test of Independence in SPSS Statistics

Let’s embark on a step-by-step guide on performing the Chi-Square Test of Independence using SPSS

1. STEP: Load Data into SPSS

Commence by launching SPSS and loading your dataset, which should encompass the variables of interest – a categorical independent variable. If your data is not already in SPSS format, you can import it by navigating to File > Open > Data and selecting your data file.

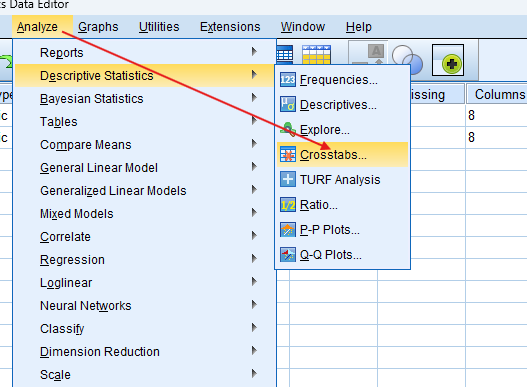
2. STEP: Access the Analyze Menu

In the top menu, click on Analyse > Descriptive Statistics > Crosstabs.

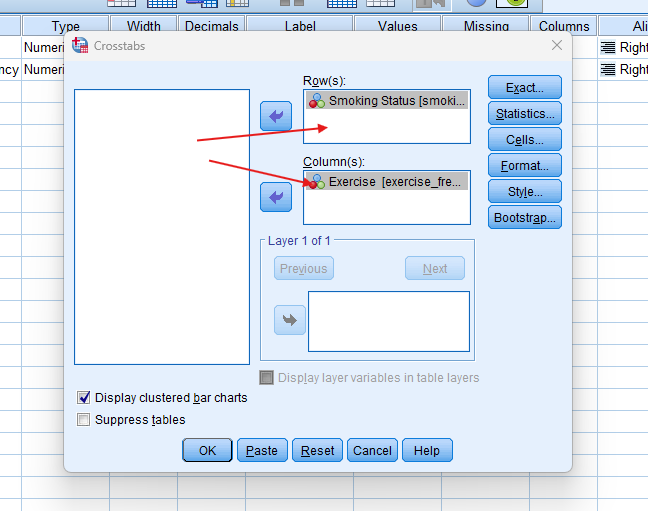
3. STEP: Specify Variables 

• Assign one variable to the row and the other to the column in the crosstabs dialogue box.
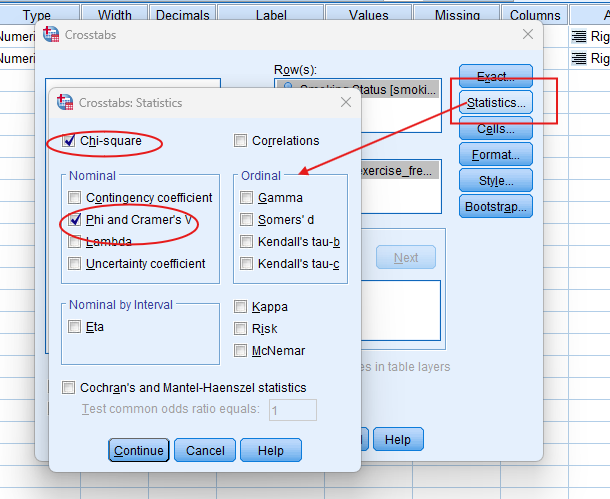
• Choose Chi-Squared: Click on the Statistics button, and select Chi-square to include the test in your output.
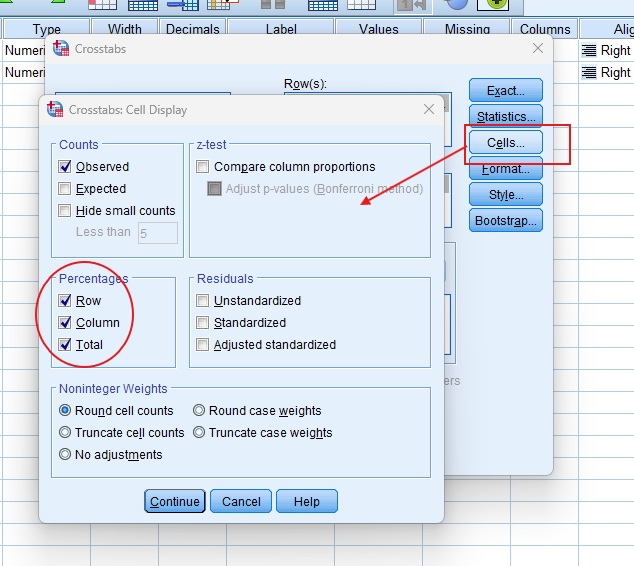
• Check Expected Counts: Enable the expected counts to compare observed and expected values.
• Check Effect Size: Choose the most appropriate effect size from the menu.

4. STEP: Generate SPSS Output

• Click ‘OK’ after selecting your variables and method. SPSS will run the analysis and generate output tables and survival curves.

Note: Conducting the Chi-Square Test of Independence in SPSS provides a robust foundation for understanding the key features of your data. Always ensure that you consult the documentation corresponding to your SPSS version, as steps might slightly differ based on the software version in use. This guide is tailored for SPSS version 25, and for any variations, it’s recommended to refer to the software’s documentation for accurate and updated instructions.

10. How to Interpret SPSS Output of Chi-Square Test of Independence 

SPSS will generate output, including the Crosstabulation Table, Chi-Square Tests, Symmetric Measures and bar plot.

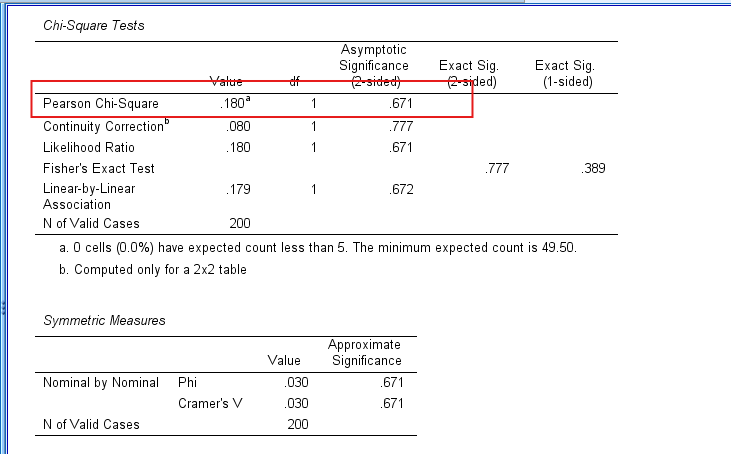
• Chi-Squared Test Table: This table provides the Chi-Square statistic, degrees of freedom (df), and the p-value. If the p-value is less than the chosen significance level (commonly 0.05).
• Crosstabulation Table: This table presents the observed and expected frequencies for each category combination of the two variables. You can also examine row and column percentages to understand the distribution of responses within each category.
• Effect Size Table (Symmetric Measures): Phi and Cramér’s V values measure the strength of the association between the two categorical variables. Values range from 0 (no association) to 1 (perfect association).
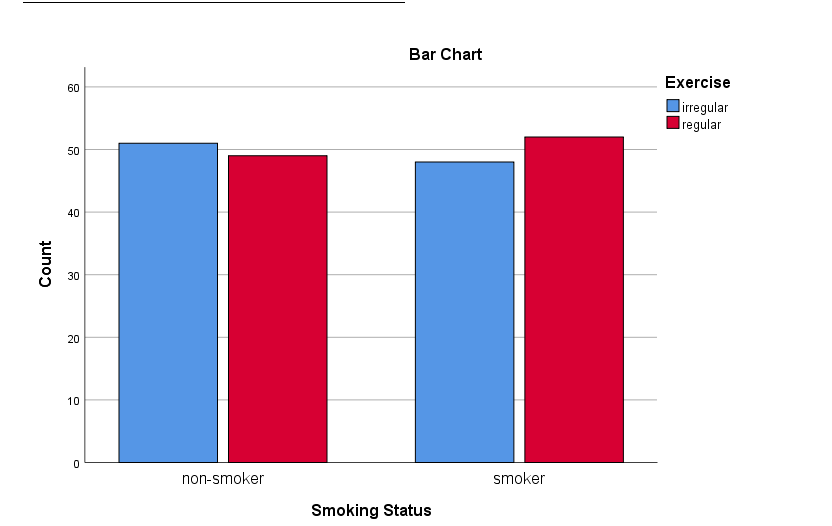
• Bar Plot: The bar plot visually compares the distribution of responses for each category of the variables.

11. How to Report Results of Chi-Square Test of Independence in APA

Reporting the results of the chi-square test in APA (American Psychological Association) format requires a structured presentation. Here’s a step-by-step guide in list format:

• Introduction: Briefly describe the purpose of the analysis and the theoretical background.
• Method: Detail the data collection process, variables used, and the model specified.
• Results: Present the parameter estimates with their standard errors, and significance levels.
• Figures and Tables: Include relevant plots and tables, ensuring they are properly labeled and referenced.
• Discussion: Interpret the results, highlighting the significance of the findings and their implications.
• Conclusion: Summarise the main points and suggest potential areas for further research.

Get Support For Your SPSS Data Analysis

Embark on a seamless research journey with SPSSAnalysis.com, where our dedicated team provides expert data analysis assistance for students, academicians, and individuals. We ensure your research is elevated with precision. Explore our pages;

• Biostatistical Modeling Expert
• Statistical Methods for Clinical Studies
• Epidemiological Data Analysis
• Biostatistical Support for Researchers
• Clinical Research Data Analysis
• Medical Data Analysis Expert
• Biostatistics Consulting
• Healthcare Data Statistics Consultant

• SPSS Help by Subjects Area: Psychology, Sociology, Nursing, Education, Medical, Healthcare, Epidemiology, Marketing 

Connect with us at SPSSAnalysis.com to empower your research endeavors and achieve impactful data analysis results. Get a FREE Quote Today!