Chi-Square Test for Association in SPSS
Discover the Chi-Square Test for Association in SPSS! Learn how to perform, understand SPSS output, and report results in APA style. Check out this simple, easy-to-follow guide below for a quick read!
Struggling with the Chi-Squared Test in SPSS? We’re here to help. We offer comprehensive assistance to students, covering assignments, dissertations, research, and more. Request Quote Now!
1. Introduction
The chi-square test for Association is a vital statistical tool for examining the relationship between two categorical variables. Researchers often use it in fields such as social sciences, biology, and marketing to determine if an association exists between two categorical factors. This test provides a way to identify whether the distribution of data in one variable is independent of another.
In this blog post, we will explore how the Chi-Square Test for Association works, how to perform it in SPSS, and how to interpret the results. Additionally, we will discuss its assumptions, hypotheses, and report the findings in APA format, making this a complete guide for using the test in your research or studies.
2. What is the Chi-Square Test for Association in Statistics?
The Chi-Square Test for Association is a non-parametric statistical test used to determine if there is a significant association between two categorical variables. It works by comparing the observed frequencies in a contingency table to the expected frequencies, which are the frequencies that would occur if the two variables were independent. The test calculates the difference between observed and expected values to determine if a significant relationship exists.
Several key terms relate to the Chi-Square Test for Association:
- Cross Tabulation: A method of summarising categorical data by displaying the frequency distribution of the variables in a matrix format.
- Contingency Table: A table used in the Chi-Square test that shows the observed frequency counts for each combination of the variables.
- Effect Sizes for Chi-Square: Effect size measures include Phi (φ), Cramér’s V, Gamma, Somers’d, and Kendall’s tau-b. These effect sizes help quantify the strength of the association.
Effect Size Chi-square Test
- Phi (φ): Phi is used when both variables in the contingency table are dichotomous (2×2 table). It measures the degree of association between two binary variables, with values ranging from -1 to +1, where values closer to ±1 indicate a stronger association.
- Cramér’s V: Cramér’s V is a generalisation of Phi and is used when the contingency table is larger than 2×2. It adjusts Phi for the size of the table and also ranges from 0 to 1, with values closer to 1 indicating a stronger association.
- Gamma: Gamma measures the strength and direction of association between two ordinal variables. It ranges from -1 to +1, where positive values indicate a positive relationship and negative values indicate an inverse relationship.
- Somers’ d: Somers’ d is an asymmetrical measure used when one variable is considered dependent. It measures the strength and direction of association between two ordinal variables, and like Gamma, it ranges from -1 to +1.
- Kendall’s tau-b: This measure is used for square contingency tables where both variables are ordinal. It adjusts for ties in the data and provides an indication of the strength and direction of the relationship between the two variables.
- Kendall’s tau-c: Similar to tau-b but used for non-square tables, tau-c adjusts for different numbers of categories in each variable.
3. What is the Formula for the Chi-Square Test?
The formula for the Chi-Square Test for Association is:
χ2=∑(O−E)2E\chi^2 = \sum \frac{(O – E)^2}{E}
Where:
- O represents the observed frequency for each category.
- E represents the expected frequency for each category, assuming no association between the variables.
The formula calculates how far the observed counts deviate from the expected counts under the null hypothesis of no association. The test result is compared against the Chi-Squared distribution to determine statistical significance.
4. What is the Chi-Square Test used for?
The chi-square test for Association is widely used in research to explore the relationship between two categorical variables. In healthcare, researchers use it to assess whether there is an association between factors like gender and disease prevalence. In marketing, it helps in determining whether there is a relationship between age groups and product preference.
This test is also useful in situations where researchers want to analyse survey data or any form of observational study that involves categorical data. By using the Chi-Square Test for Association, one can assess whether variables are associated or independent, making it a crucial tool in decision-making and scientific inquiry.
5. Explain Differences among Chi-Square Tests of Independence, Goodness Fit, Association and Homogeneity
- Chi-Square Test for Association: Determines if two categorical variables are associated or independent by comparing observed and expected frequencies in a contingency table.
- Chi-Square Test of Independence: Similar to the test for association, it assesses whether two variables are independent. The key difference lies in the context of the research question, with independence tests often focusing on whether the distribution of one variable is unaffected by the other.
- Chi-Square Goodness-of-Fit Test: Compares observed frequencies of a single categorical variable to a theoretically expected distribution. Researchers use it to determine if a sample fits a specific distribution.
- Chi-Square Test of Homogeneity: Tests whether two or more groups are homogeneous in terms of the distribution of a categorical variable. This test is used to compare the proportions across different populations.
- Fisher’s Exact Test: Fisher’s Exact Test is an alternative to the Chi-Squared test for 2×2 contingency tables, especially when sample sizes are small or when expected frequencies are less than 5. Unlike the Chi-Squared test, Fisher’s Exact Test provides an exact p-value, making it more accurate when dealing with small or sparse data. It is particularly useful when the assumptions of the Chi-Squared test are not met.
6. What are the Assumptions of the Chi-Square Test?
Before performing the Chi-Square Test for Association, researchers must ensure that certain assumptions are met. Failing to meet these assumptions may lead to inaccurate results, so it is essential to understand and verify them before proceeding with the analysis.
- The variables must be categorical.
- The observations must be independent of one another.
- The expected frequency in each cell of the contingency table should be 5 or greater.
- The sample size should be sufficiently large to ensure reliable results.
- The data should not contain overlapping categories.
7. What is the Hypothesis of the Chi-Square Test?
The hypotheses for the Chi-Square Test for Association are:
- Null Hypothesis (H₀): There is no association between the two categorical variables. In other words, the variables are independent.
- Alternative Hypothesis (H₁): There is an association between the two categorical variables. The variables are dependent on one another.
Rejecting the null hypothesis indicates that a statistically significant association exists between the two variables.
8. An Example of the Chi-Square Test for Association
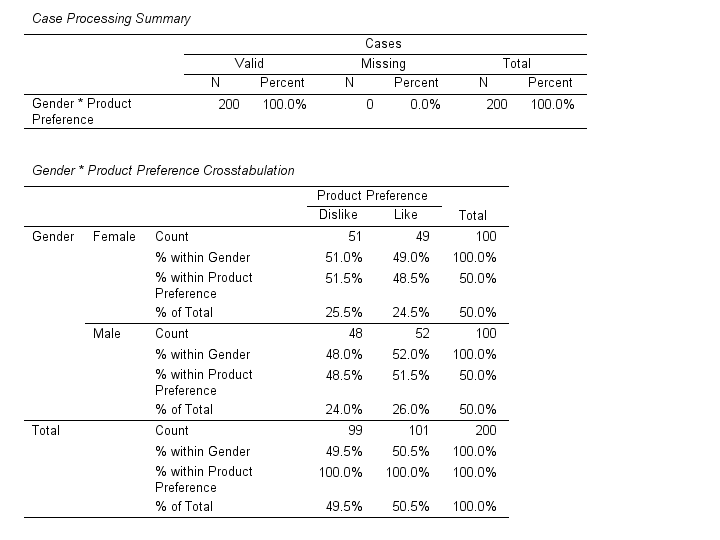
Consider a study investigating the relationship between gender and preference for a new product. The two categorical variables are gender (male and female) and product preference (like and dislike). The researcher collects data from a survey of 200 respondents, cross-tabulating the responses to create a contingency table.
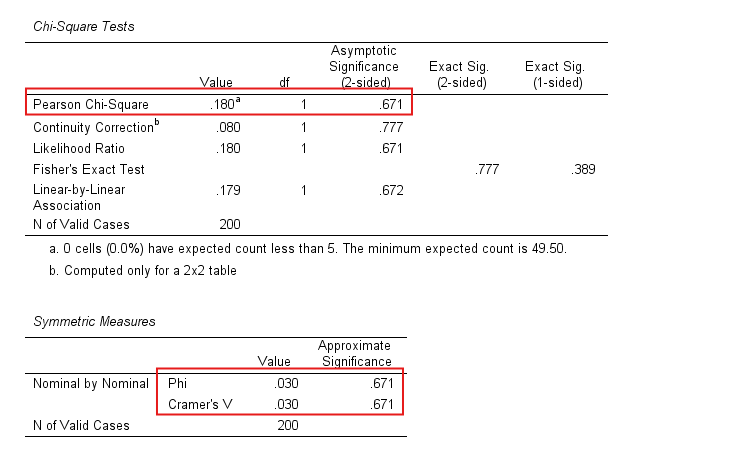
Using the Chi-Square Test for Association, the researcher compares the observed frequencies of responses with the expected frequencies (assuming no association). If the Chi-Squared test statistic exceeds the critical value from the Chi-Squared distribution table, the researcher concludes that gender is significantly associated with product preference.
9. How to Perform Chi Square Test for Association in SPSS
Step by Step: Running Chi-Square Test for Association in SPSS Statistics
Let’s embark on a step-by-step guide on performing the Chi-Square Test for Association using SPSS
- STEP: Load Data into SPSS
Commence by launching SPSS and loading your dataset, which should encompass the variables of interest – a categorical independent variable. If your data is not already in SPSS format, you can import it by navigating to File > Open > Data and selecting your data file.
- STEP: Access the Analyze Menu
In the top menu, click on Analyse > Descriptive Statistics > Crosstabs.
- STEP: Specify Variables
- Assign one variable to the row and the other to the column in the crosstabs dialogue box.
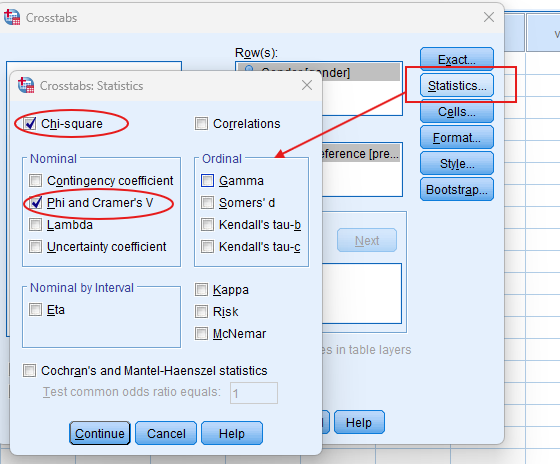
- Choose Chi-Squared: Click on the Statistics button, and select Chi-square to include the test in your output.
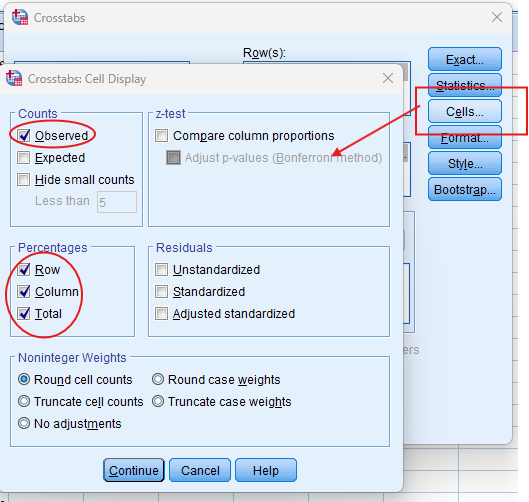
- Check Expected Counts: Enable the expected counts to compare observed and expected values.
- Check Effect Size: Choose the most appropriate effect size from the menu.
- STEP: Generate SPSS Output
- Click ‘OK’ after selecting your variables and method. SPSS will run the analysis and generate output tables and survival curves.
Note: Conducting the Chi-Square Test for Association in SPSS provides a robust foundation for understanding the key features of your data. Always ensure that you consult the documentation corresponding to your SPSS version, as steps might slightly differ based on the software version in use. This guide is tailored for SPSS version 25, and for any variations, it’s recommended to refer to the software’s documentation for accurate and updated instructions.
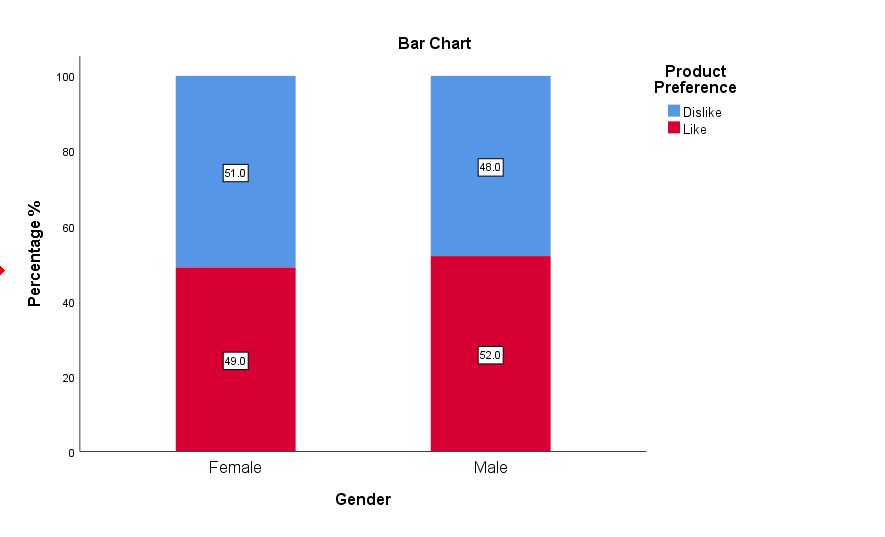
SPSS Output for Chi Square Test for Association
10. How to Interpret SPSS Output of Chi-Square Test for Association
SPSS will generate output, including the Crosstabulation Table, Chi-Square Tests, Symmetric Measures and bar plot.
- Chi-Squared Test Table: This table provides the Chi-Square statistic, degrees of freedom (df), and the p-value. If the p-value is less than the chosen significance level (commonly 0.05).
- Crosstabulation Table: This table presents the observed and expected frequencies for each category combination of the two variables. You can also examine row and column percentages to understand the distribution of responses within each category.
- Effect Size Table (Symmetric Measures): Phi and Cramér’s V values measure the strength of the association between the two categorical variables. Values range from 0 (no association) to 1 (perfect association).
- Bar Plot: The bar plot visually compares the distribution of responses for each category of the variables.
11. How to Report Results of Chi-Square Test for Association in APA
Reporting the results of the chi-square test for association in APA (American Psychological Association) format requires a structured presentation. Here’s a step-by-step guide in list format:
- Introduction: Briefly describe the purpose of the analysis and the theoretical background.
- Method: Detail the data collection process, variables used, and the model specified.
- Results: Present the parameter estimates with their standard errors, and significance levels.
- Figures and Tables: Include relevant plots and tables, ensuring they are properly labeled and referenced.
- Discussion: Interpret the results, highlighting the significance of the findings and their implications.
- Conclusion: Summarise the main points and suggest potential areas for further research.

Get Support For Your SPSS Data Analysis
Embark on a seamless research journey with SPSSAnalysis.com, where our dedicated team provides expert data analysis assistance for students, academicians, and individuals. We ensure your research is elevated with precision. Explore our pages;
- Biostatistical Modeling Expert
- Statistical Methods for Clinical Studies
- Epidemiological Data Analysis
- Biostatistical Support for Researchers
- Clinical Research Data Analysis
- Medical Data Analysis Expert
- Biostatistics Consulting
- Healthcare Data Statistics Consultant
- SPSS Help by Subjects Area: Psychology, Sociology, Nursing, Education, Medical, Healthcare, Epidemiology, Marketing
Connect with us at SPSSAnalysis.com to empower your research endeavors and achieve impactful data analysis results. Get a FREE Quote Today!