Structural Equation Analysis

Introduction

Structural Equation Modeling (SEM) represents a comprehensive statistical approach used to assess the relationships among multiple variables. Researchers and analysts often use this method in social sciences, behavioural sciences, and other disciplines to understand complex phenomena. Using SPSS AMOS, one can develop and test these models efficiently. SEM facilitates the examination of intricate models that include multiple dependent variables and interrelated constructs, making it an invaluable tool for sophisticated data analysis.

In this blog post, we will explore the Structural Equation Analysis (SEM) or Structural Equation Analysis in SPSS AMOS. We will cover key concepts, the SEM framework, and guide you through a step-by-step process for performing SEM in SPSS AMOS. Additionally, we will discuss how to interpret the output and report results in APA style. By the end of this article, you should have a solid understanding of how to use SEM to enhance your research and data analysis capabilities.

1. What is Structural Equation Analysis in SPSS AMOS?

Structural Equation Analysis in SPSS AMOS allows researchers to assess and model basic relationships among observed and latent variables. SEM integrates multiple regression analysis, path analysis and confirmatory factor analysis, enabling the simultaneous analysis of multiple pathways. By using SEM, researchers can construct models that represent theoretical constructs and validate them with empirical data.

Structural Equation Analysis stands out due to its ability to handle multiple dependent variables and account for measurement errors, which traditional regression methods often overlook. Researchers can specify models that reflect theoretical constructs, estimate the parameters, and evaluate the fit of the model using various goodness-of-fit indices. This method’s flexibility and robustness make it an essential tool in social sciences, psychology, education, and other fields where understanding complex relationships is crucial.

SPSS AMOS, a powerful add-on module for SPSS, is designed specifically for SEM. It provides a user-friendly graphical interface that simplifies the process of model specification, estimation, and testing. Through AMOS, users can draw path diagrams, specify models, and obtain detailed output that helps in the thorough evaluation of the proposed model. This combination of SEM and SPSS AMOS offers a robust framework for conducting sophisticated statistical analysis.

2. Structural Equation Analysis: Some Definitions

• Observed Variable: An observed variable is a measurable variable in a study, directly recorded from respondents. It serves as a foundational element in SEM, representing tangible data points.
• Latent Variable: A latent variable is not directly observable but inferred from observed variables. These variables represent underlying constructs, such as intelligence or satisfaction.
• Exogenous Variable: Exogenous variables are independent variables within SEM, not influenced by other variables in the model. They serve as predictors or determinants of other variables.
• Endogenous Variable: Endogenous variables are dependent variables influenced by one or more exogenous variables. They act as outcomes or effects within the model.
• Measurement Model: The measurement model specifies the relationships between observed variables and their underlying latent constructs. It essentially forms the basis of factor analysis within SEM.
• Indicator: An indicator is an observed variable used to define a latent variable. Indicators are essential for the measurement of latent constructs.
• Factor: A factor represents a latent variable in the model, underlying the observed variables. Factors illustrate how observed data reflect abstract constructs.
• Loading: Loadings are coefficients that show the relationship strength between observed variables and their corresponding latent variables. Higher loadings indicate a stronger relationship.
• Structural Model: The structural model defines the relationships between latent variables. It shows how constructs interact and influence each other within the SEM framework.
• Regression Path: A regression path represents the directional influence between variables in the model. It depicts causal relationships and the flow of influence within SEM.

3. What is the difference among CFA, SEM, Path Analysis, and Multiple Regression?

3.1. Confirmatory Factor Analysis (CFA)

• Purpose: Confirmatory Factor Analysis (CFA) tests whether a set of observed variables represents a number of underlying latent constructs. It verifies the factor structure hypothesised in the theory.
• Focus: It focuses on the measurement model, ensuring that the observed variables are accurate indicators of the latent variables.
• Model Specification: Researchers specify which observed variables load onto which latent variables before the analysis.
• Outcome: Provides information on factor loadings, model fit indices, and modification indices to improve the model.

3.2.Path Analysis

• Purpose: Path analysis assesses the direct and indirect relationships between observed variables, focusing on the structural relationships without latent constructs.
• Focus: It analyses causal relationships among variables through a series of regression equations.
• Model Specification: Researchers specify the directional paths among observed variables.
• Outcome: Provides path coefficients that indicate the strength and significance of the relationships.

3.3. Structural Equation Modelling (SEM)

• Purpose: SEM integrates both the measurement model (CFA) and the structural model (path analysis) to evaluate complex relationships between observed and latent variables.
• Focus: It examines causal relationships among multiple variables, including direct and indirect effects.
• Model Specification: SEM requires specifying both the measurement model and the structural paths between latent variables.
• Outcome: Offers comprehensive insights into the model fit, path coefficients, and overall model validity.

3.4. Multiple Regression

• Purpose: Multiple regression predicts the value of a dependent variable based on several independent variables.
• Focus: It examines the linear relationships between the dependent variable and independent variables.
• Model Specification: Researchers specify one dependent variable and multiple independent variables without considering latent constructs.
• Outcome: Provides coefficients indicating the contribution of each independent variable to the prediction of the dependent variable.

Understanding these differences helps researchers choose the appropriate statistical technique based on their research questions and data characteristics. Each method offers unique insights, contributing to a more comprehensive understanding of the relationships within the data. Here, you can decide your sem model using the following diagram;

Please visit our following posts for other models:  Simple Linear Regression, Hierarchical Regression, Multiple Linear Regression, CFA

4. Model Indices for Structural Equation Analysis (SEM)

Acceptable fit indices provide benchmarks for determining whether a structural equation model adequately fits the data. Generally, a good fit is indicated by a Chi-Square (Chisq) value that is non-significant, although this is sensitive to sample size. Goodness of Fit Index (GFI) and Adjusted Goodness of Fit Index (AGFI) values should exceed 0.90 for a good fit.

Comparative Fit Index (CFI) and Tucker-Lewis Index (TLI) values above 0.95 indicate an excellent fit, while values above 0.90 are considered acceptable. Root Mean Square Error of Approximation (RMSEA) values below 0.06 indicate a close fit, with values up to 0.08 representing a reasonable error of approximation. Standardized Root Mean Square Residual (SRMR) values less than 0.08 are generally indicative of a good model fit.

5. What are the Assumptions of Structural Equation Analysis?

• Linearity: The relationships among variables are linear.
• Normality: Variables are normally distributed.
• Independence: Observations are independent.
• Measurement Error: Measurement errors are uncorrelated.
• Model Specification: The model is correctly specified.
• Sample Size: Adequate sample size for reliable results.
• Multicollinearity: No perfect multicollinearity among exogenous variables.
• Identification: The model is identifiable, meaning a unique solution can be obtained.
• Model Fit: The model adequately fits the data.
• Path Coefficients: Path coefficients are stable across different samples.

6. What is the Hypothesis of Structural Equation Analysis?

In a Structural Equation Analysis, hypotheses are statements about the relationships between variables. Researchers formulate these hypotheses based on theoretical frameworks and prior research. A typical hypothesis might state that a latent variable significantly predicts an observed outcome. For instance, one might hypothesise that job satisfaction (latent variable) positively influences job performance (observed variable).

Hypotheses in SEM often involve testing the significance of path coefficients, which represent the strength and direction of relationships. For example, a hypothesis might assert that the path coefficient from job satisfaction to job performance is positive and statistically significant. Researchers use SPSS AMOS to estimate these coefficients and test the hypotheses, examining the empirical support for the theoretical model. This process helps in validating the proposed relationships and refining the theoretical constructs.

7. An Example of Structural Equation Analysis

Consider a study aiming to understand how emotional disorders influence depression among adults. Researchers propose a model where emotional disorders and depression are latent variables, each measured by five Likert-scale items. The study hypothesises that emotional disorders significantly predict levels of depression.

Firstly, researchers define the measurement model. For emotional disorders, the five Likert items might include questions like “I often feel anxious” and “I struggle with mood swings.” For depression, the items could be “I feel sad frequently” and “I have trouble enjoying activities.” These items serve as indicators of their respective latent constructs.

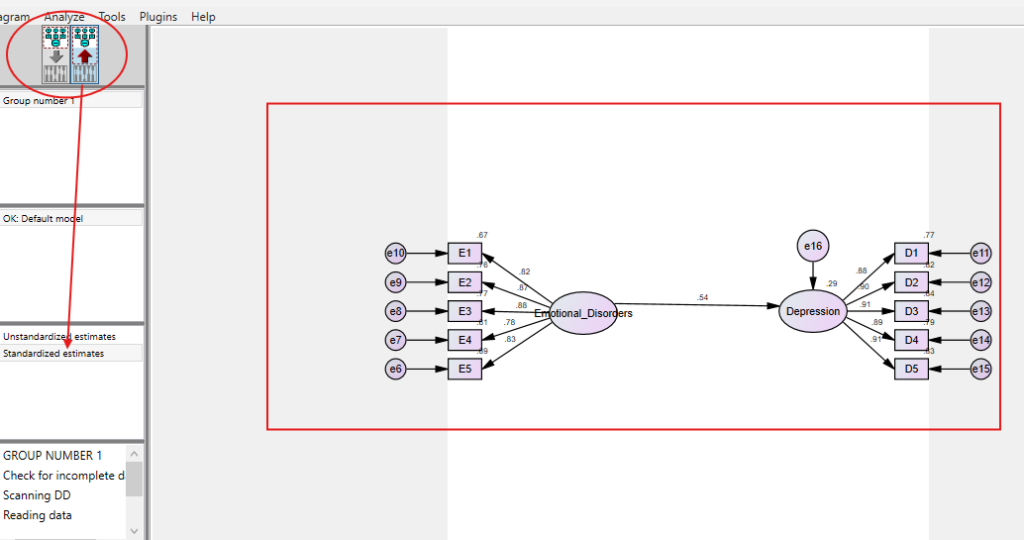
Using SPSS AMOS, researchers construct the model by specifying the relationships between the latent variables (emotional disorders and depression). The path diagram illustrates how emotional disorders, as a latent variable, influence depression. Researchers would then collect data, input it into SPSS, and use AMOS to estimate the model’s parameters. The output provides insights into how strongly emotional disorders impact depression, helping psychologists and mental health professionals develop better intervention strategies.

Step by Step: Running Structural Equation Analysis in SPSS AMOS

Let’s embark on a step-by-step guide on performing the SEM using SPSS AMOS

1. Define Variables: Start by defining the observed and latent variables in your model. Here, the latent variables are emotional disorders and depression, each measured by five Likert-scale items.
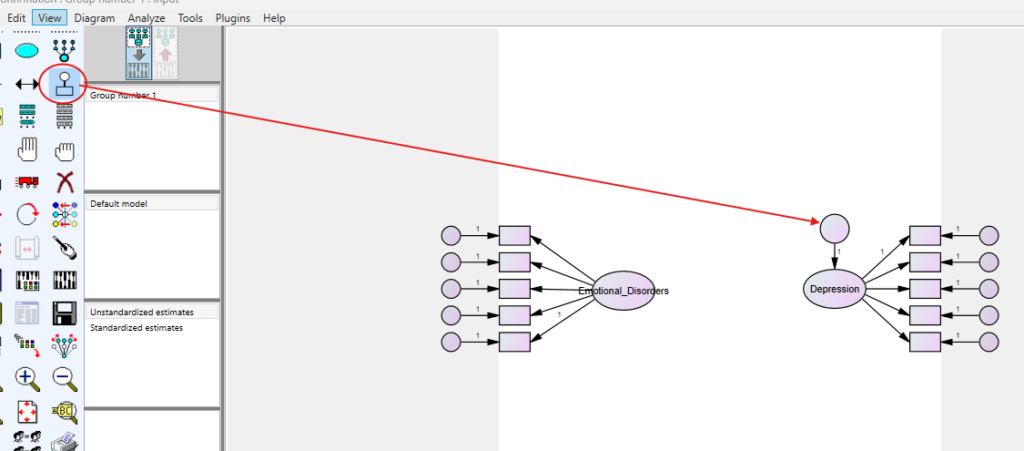
2. Draw Path Diagram: Use AMOS’s graphical interface to draw the path diagram. Depict emotional disorders as a latent variable with arrows pointing to its five observed indicators. Similarly, depict depression with its five indicators. Draw an arrow from emotional disorders to depression to represent the hypothesised predictive relationship.
3. Specify Model: Input the paths and correlations between variables in the diagram. Ensure that each observed item correctly loads onto its respective latent construct.
4. Input Data: Load your dataset into SPSS and link it to AMOS.
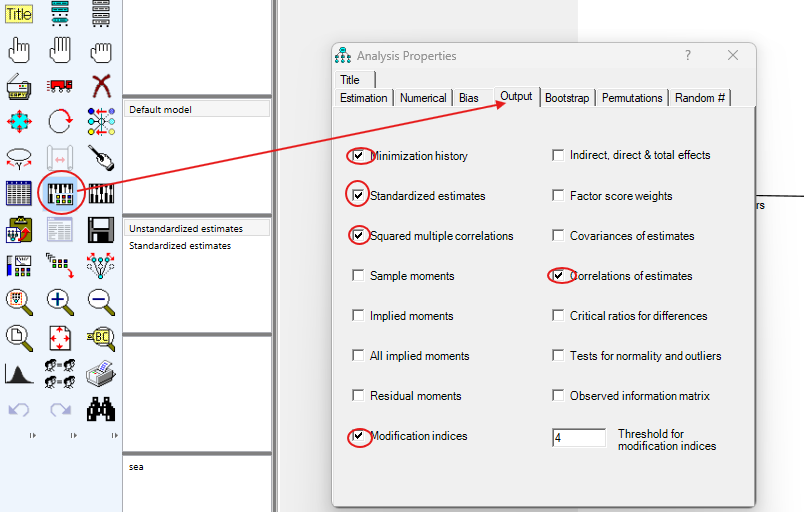
5. Estimate Model: Run the estimation process to obtain path coefficients and model fit indices.
6. Evaluate Fit: Check the goodness-of-fit indices, such as Chi-square, RMSEA, CFI, and TLI, to assess how well the model fits the data. Ensure the values meet acceptable thresholds.
7. Refine Model: Modify the model based on the fit indices and theoretical considerations if necessary.
8. Interpret Results: Analyse the output to understand the relationships and their significance.

How to Interpret SPSS AMOS Output of Structural Equation Analysis

When interpreting the SPSS AMOS output for a Structural Equation Analysis, focus on several key components. Firstly, examine the path coefficients, which indicate the strength and direction of the relationships between variables. Significant path coefficients suggest meaningful relationships, while non-significant ones may need re-evaluation. Secondly, review the goodness-of-fit indices, such as the Chi-square test, RMSEA, CFI, and TLI, to determine how well the model fits the data.

Additionally, consider the standardised residuals and modification indices. Standardised residuals help identify any discrepancies between observed and predicted values, pointing out areas where the model may not fit well. Modification indices suggest potential adjustments to improve model fit, such as adding or removing paths. By carefully analysing these outputs, researchers can validate their theoretical models and ensure robust conclusions.

How to Report Results of Structural Equation Analysis in APA

1. Model Description: Describe the theoretical model and the hypothesised relationships.
2. Data Collection: Explain the data collection process and sample characteristics.
3. Model Specification: Detail how the model was specified, including the paths and variables.
4. Goodness-of-Fit: Report the goodness-of-fit indices, including Chi-square, RMSEA, CFI, and TLI.
5. Path Coefficients: Present the path coefficients with their significance levels.
6. Model Modifications: Discuss any modifications made to improve model fit.
7. Interpretation: Interpret the results, highlighting key findings and their implications.
8. Tables and Figures: Include tables of path coefficients and figures of the path diagram.
9. Conclusion: Summarise the findings and their relevance to the research question.

Get Help For Your SPSS Analysis

Embark on a seamless research journey with SPSSAnalysis.com, where our dedicated team provides expert data analysis assistance for students, academicians, and individuals. We ensure your research is elevated with precision. Explore our pages;

• SPSS Help by Subjects Area: Psychology, Sociology, Nursing, Education, Medical, Healthcare, Epidemiology, Marketing 
• Dissertation Methodology Help
• Dissertation Data Analysis Help
• Dissertation Results Help
• Pay Someone to Do My Data Analysis
• Hire a Statistician for Dissertation
• Statistics Help for DNP Dissertation
• Pay Someone to Do My Dissertation Statistics

Connect with us at SPSSAnalysis.com to empower your research endeavors and achieve impactful data analysis results. Get a FREE Quote Today!