Spearman’s Rho Correlation in SPSS

Introduction

Understanding the dynamics between variables is a crucial aspect of statistical analysis, and Spearman’s Rho Correlation provides a valuable tool for assessing relationships when faced with non-parametric data. In the realm of statistical exploration, Spearman’s Rho offers an alternative to Pearson correlation, particularly suitable for ordinal or non-normally distributed data.

This blog post delves into the intricacies of Spearman’s Rho Correlation in SPSS, shedding light on its applications and the underlying assumptions that pave the way for robust analyses. Whether you’re a seasoned statistician or a newcomer to data analysis, this exploration aims to demystify the method and empower you with the knowledge to navigate its implementation effectively.

What are the 5 Correlation Analyses?

Correlation Analysis offers various methods to explore associations between variables. Besides the commonly used Pearson Correlation, others include Spearman’s Rho rank order, Kendall’s Tau, Partial Correlation, and Canonical Correlation.

1. Pearson Correlation Analysis

• Description: Measures the linear relationship between two continuous variables.
• Applicability: Best suited for variables with a linear association and normally distributed data.
• Range: Correlation coefficient (r) ranges from -1 to 1.
• Interpretation: Positive values indicate a positive linear relationship, negative values indicate a negative linear relationship, and 0 implies no linear relationship.

2. Spearman Rank-Order Correlation

• Description: Non-parametric measure assessing the monotonic relationship between two variables.
• Applicability: Suitable for ordinal data or when assumptions of normality are violated.
• Procedure: Converts data into ranks and compute the correlation based on the rank differences.
• Interpretation: The correlation coefficient (rho) ranges from -1 to 1, with a similar interpretation to Pearson.

3. Kendall’s Tau

• Description: Non-parametric measure assessing the strength and direction of a monotonic relationship.
• Applicability: Similar to Spearman, suitable for ordinal data and non-normally distributed data.
• Procedure: Measures the number of concordant and discordant pairs in the data.
• Interpretation: Kendall’s Tau (τ) ranges from -1 to 1, with 0 indicating no association and values towards -1 or 1 indicating stronger associations.

4. Partial Correlation

• Description: Examines the relationship between two variables while controlling for the influence of one or more additional variables.
• Applicability: Useful when there is a need to isolate the direct relationship between two variables.
• Procedure: Calculates the correlation between two variables after removing the shared variance with the control variable(s).
• Interpretation: Provides insights into the unique contribution of each variable to the correlation.

5. Canonical Correlation

• Description: Assesses the association between two sets of variables.
• Applicability: Useful when dealing with multiple sets of variables simultaneously.
• Procedure: Maximizes the correlation between linear combinations of variables from each set.
• Interpretation: Provides information on the overall relationship between sets of variables, producing canonical correlation coefficients.

Understanding the characteristics and applications of each correlation analysis method equips researchers with a versatile toolkit for exploring diverse data scenarios.

Spearman’s Rho Correlation

Spearman’s Rho Correlation, named after Charles Spearman, is a non-parametric measure of statistical dependence between two variables. Unlike Pearson correlation, Spearman’s Rho assesses the strength and direction of monotonic relationships, making it suitable for ordinal data or situations where the assumption of linearity is not met. Spearman’s Rho is calculated based on the ranks of the data, transforming raw scores into ranks before computing the correlation coefficient. This method provides a robust solution for scenarios where variables may exhibit a consistent trend without adhering strictly to linear patterns.

In the subsequent sections, we’ll delve into the mechanics of Spearman’s Rho Correlation, exploring its applications and the key assumption considerations for meaningful analyses in SPSS.

Correlation Coefficient

At the heart of Spearman’s Rho Correlation lies the correlation coefficient, a numerical index that quantifies the strength and direction of a relationship between two variables. In the case of Spearman’s Rho, the coefficient is calculated based on the rank order of data values rather than their actual numeric values. The correlation coefficient ranges between -1 and 1, where -1 indicates a perfect negative monotonic relationship, 1 indicates a perfect positive monotonic relationship, and 0 signifies no monotonic relationship. This numerical measure becomes a valuable indicator for researchers and analysts aiming to understand the association between variables in a more nuanced manner, especially when faced with data that does not meet the assumptions of parametric analyses.

Assumptions of Spearman’s Rho Correlation

Before delving into Spearman’s Rho Correlation in SPSS, it’s crucial to be aware of the assumptions that underpin its validity. Unlike parametric tests, Spearman’s Rho doesn’t require assumptions of normality or homoscedasticity.

• Ordinal or Interval Scale: The variables under analysis should be measured on an ordinal or interval scale. Spearman’s Rho is well-suited for variables with ordinal properties.
• Independence: The observations should be independent of each other. This assumption is particularly important when dealing with paired data points.
• Extreme Outliers: While Spearman’s Rho is robust to outliers, extreme values can still influence the correlation. Checking for and addressing outliers is advisable.
• No Ties in Data: If there are tied ranks in the data (two or more observations with the same value), adjustments may be needed to the correlation coefficient calculation.

Understanding and adhering to these assumptions is crucial for the meaningful application of Spearman’s Rho Correlation Analysis in SPSS. It ensures the reliability and validity of the results, providing a solid foundation for interpreting the relationships between variables in non-parametric settings.

 Hypothesis of Spearman’s Rho Analysis

When formulating hypotheses for Spearman’s Rho Correlation Analysis, researchers typically consider the null hypothesis (H0) and the alternative hypothesis (H1).

• The null hypothesis: there is no significant relationship between the two variables.
• The alternative hypothesis: there is a significant relationship between the variables.

Researchers are interested in determining whether the correlation coefficient in the sample is significantly different from zero. The formulation of clear hypotheses is integral to guiding the analysis and drawing meaningful conclusions about the nature of the relationship between the variables under investigation.

Example of Spearman’s Rho Correlation

A researcher is interested in examining the relationship between the number of hours spent exercising per week and the level of physical fitness in a sample of individuals. The data collected includes the weekly exercise hours (variable X) and a physical fitness score determined through a standardized test (variable Y).

• Null Hypothesis: There is no significant relationship between the number of hours spent exercising per week and the level of physical fitness in the population.
• Alternative Hypothesis: There is a significant relationship between the number of hours spent exercising per week and the level of physical fitness in the population.

Conducting a Spearman’s Rho Correlation Analysis on this data will involve testing these hypotheses to determine whether there is a statistically significant linear relationship between exercise hours and physical fitness scores in the given sample. The results will guide conclusions about the strength and direction of this relationship.

Step by Step: Running Spearman’s Rho Correlation in SPSS Statistics

Now, let’s delve into the step-by-step process of conducting the Spearman’s Rho Correlation using SPSS.  Here’s a step-by-step guide on how to perform a Spearman’s Rho Correlation Analysis in SPSS:

1. STEP: Load Data into SPSS

Commence by launching SPSS and loading your dataset, which should encompass the variables of interest – a categorical independent variable. If your data is not already in SPSS format, you can import it by navigating to File > Open > Data and selecting your data file.

2. STEP: Access the Analyze Menu

In the top menu, locate and click on “Analyze.” Within the “Analyze” menu, navigate to “Correlate” and choose ” Bivariate” Analyze > Correlate> Bivariate

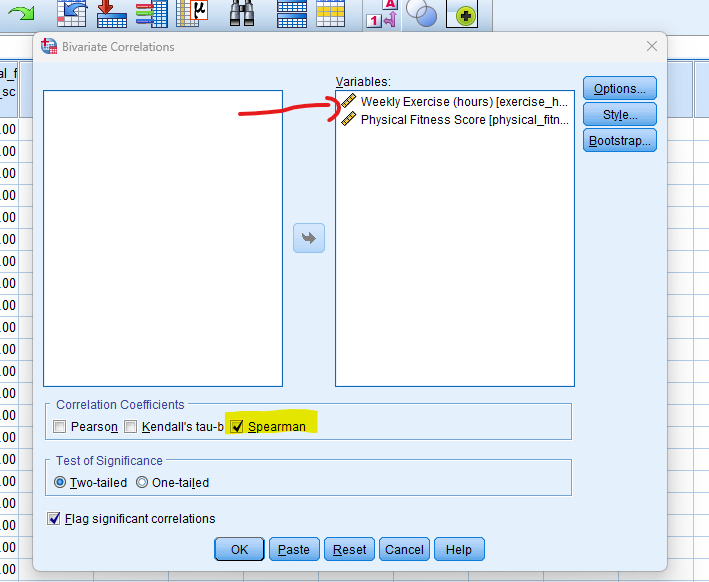
3. STEP: Choose Variables

– In the “Bivariate Correlations” dialogue box, select the variables you want to analyze. Move the variables of interest from the list of available variables to the “Variables” box.

– Check Spearmans for Correlation Coefficient.

4. STEP: Generate SPSS Output

Once you have specified your variables and chosen options, click the “OK” button to perform the analysis. SPSS will generate a comprehensive output, including the requested frequency table and chart for your dataset.

Executing these steps initiates Spearman’s Rho Correlation Analysis in SPSS, allowing researchers to assess the impact of the teaching method on students’ test scores while considering the repeated measures. In the next section, we will delve into the interpretation of SPSS output for Spearman’s Rho Correlation Analysis.

Note

Conducting a Spearman’s Rho Correlation Analysis in SPSS provides a robust foundation for understanding the key features of your data. Always ensure that you consult the documentation corresponding to your SPSS version, as steps might slightly differ based on the software version in use. This guide is tailored for SPSS version 25, and any variations, it’s recommended to refer to the software’s documentation for accurate and updated instructions.

How to Interpret SPSS Output of Spearman’s Rho Correlation

Interpreting the SPSS output of Spearman’s Rho Correlation Analysis involves examining the correlation matrix and associated statistics. The correlation matrix displays the correlation coefficients (r) between pairs of variables. Each cell in the matrix corresponds to the correlation between two variables, and the diagonal contains the correlation of each variable with itself, which is always 1. The correlation coefficient ranges from -1 to 1, with values closer to 1 or -1 indicating a stronger linear relationship.

Key elements to interpret in the output include:

• Correlation Coefficient (rho): The strength and direction of the linear relationship.
• Significance (p-value): Indicates whether the observed correlation is statistically significant.
• Sample Size (N): The number of data points used in the analysis.

How to Report Results of Spearman’s Rho Correlation Analysis in APA

Reporting results in APA format involves providing key information such as the correlation coefficient (r), degrees of freedom, significance level, and sample size. For instance:

• Introduction: Begin by introducing the analysis, mentioning that a Spearman’s Rho correlation analysis was conducted to examine the relationships between the specified variables.
• Correlation Coefficients: Report the Spearman’s Rho correlation coefficients (rho) for each pair of variables. Clearly state which variables were analysed and provide the numerical values.
• Significance Levels: Indicate the significance levels (p-values) associated with each correlation coefficient. This helps determine whether the observed correlations are statistically significant.
• Interpretation: Interpret the strength and direction of each correlation coefficient. Use terms such as “strong,” “moderate,” or “weak” to describe the magnitude of the relationship.
• Descriptive Statistics (Optional): Present descriptive statistics for each variable, including means, standard deviations, and sample sizes. This provides context for the correlation results.
• Confidence Intervals (Optional): If confidence intervals were calculated, report them to provide a range of values within which the true population correlation is likely to fall.
• Limitations (Optional): Acknowledge any limitations of the analysis, such as potential confounding variables or the cross-sectional nature of the data.

Get Help For Your SPSS Analysis

Embark on a seamless research journey with SPSSAnalysis.com, where our dedicated team provides expert data analysis assistance for students, academicians, and individuals. We ensure your research is elevated with precision. Explore our pages;

• SPSS Data Analysis Help – SPSS Helper,
• Quantitative Analysis Help,
• Qualitative Analysis Help,
• SPSS Dissertation Analysis Help,
• Dissertation Statistics Help,
• Statistical Analysis Help,
• Medical Data Analysis Help.

Connect with us at SPSSAnalysis.com to empower your research endeavors and achieve impactful results. Get a Free Quote Today!