One Sample T Test in SPSS

Introduction

Welcome to our comprehensive guide on the One Sample t Test in SPSS, a powerful statistical tool that allows researchers to draw meaningful conclusions from a single sample of data. Statistical analysis is a crucial aspect of research, providing the means to validate hypotheses and make informed decisions. In this post, we will navigate through the fundamental aspects of the One Sample t Test, exploring its purpose, assumptions, hypothesis formulation, and practical application through a step-by-step guide in SPSS. Whether you’re a seasoned researcher or a student embarking on your statistical journey, this guide aims to demystify the complexities of the One Sample t Test and equip you with the knowledge needed to confidently analyse and interpret your data.

What is One Sample t Test?

Firstly, let’s delve into the core concept – the One Sample t Test. In essence, this statistical test assesses whether the mean of a single sample significantly differs from a known or hypothesised population mean. It is particularly useful when working with a limited dataset, making it a valuable tool for researchers across various disciplines.

The One Sample t Test provides insights into whether observed differences are statistically significant, helping researchers make informed inferences about the broader population. By examining the mean and variability of a single sample, statisticians can draw meaningful conclusions, laying the foundation for robust and credible research outcomes. In the upcoming sections, we will explore the intricacies of the One Sample t Test, from its underlying assumptions to the step-by-step process of conducting the test using the popular statistical software, SPSS.

Assumption of One Sample Test

Before delving into the intricacies of the One Sample t Test, it’s crucial to understand its underlying assumptions. The One Sample t Test, like many statistical tests, relies on certain assumptions for valid results. Here are the key assumptions of the One Sample t Test:

1. Normality: The data within the sample should follow a normal distribution. However, the One Sample t Test is robust to violations of normality, especially with larger sample sizes (typically n > 30). For smaller samples, normality is more critical, but deviations can be acceptable depending on the context.
2. Scale of Measurement: The data should be measured on at least an interval scale. This means that the data points should have meaningful intervals between them, and the concept of zero should be meaningful (although it doesn’t have to be an absolute zero).
3. Random Sampling: The sample should be a random and representative subset of the population. This ensures that the findings from the sample can be generalized to the larger population.
4. Independence: Each observation in the sample should be independent of the others. This assumption is violated if the values in the sample are somehow related or dependent on each other.

By acknowledging and validating these assumptions, researchers can enhance the reliability and validity of their statistical analyses, reinforcing the robustness of the conclusions drawn from the One Sample t Test.

The hypothesis of One-Sample t-Test:

Next, let’s unravel the formulation of hypotheses in the Sample t Test.

• The null hypothesis (H₀): there is no significant difference between the mean of the sample and the population mean.
• The alternative hypothesis (H₁): there is a significant difference between the mean of the sample and the population mean.

Example of One Sample T Test

To provide a concrete illustration of the One Sample t Test, let’s consider a scenario involving a pharmaceutical company testing the effectiveness of a new drug designed to lower blood pressure. The company has historical data indicating that the average systolic blood pressure in the general population is 120 mm Hg.

• The null hypothesis in this case would state that the new drug has no significant effect, meaning that the average systolic blood pressure for individuals taking the drug is equal to the population mean (120 mm Hg).
• The alternative hypothesis would suggest a significant difference, indicating that the drug influences blood pressure.

By performing a One Sample t Test, the pharmaceutical company can assess whether the observed mean is significantly different from the known population mean of 120 mm Hg, providing valuable insights into the drug’s efficacy. In the subsequent sections, we will guide you through the step-by-step process of conducting and interpreting the One Sample t Test using SPSS, enhancing your ability to derive meaningful conclusions from such analyses.

Step by Step: Running One Sample t Test in SPSS Statistics

Let’s embark on a step-by-step guide on performing the One Sample t Test using SPSS

1. STEP: Load Data into SPSS

Commence by launching SPSS and loading your dataset, which should encompass the variables of interest – a categorical independent variable. If your data is not already in SPSS format, you can import it by navigating to File > Open > Data and selecting your data file.

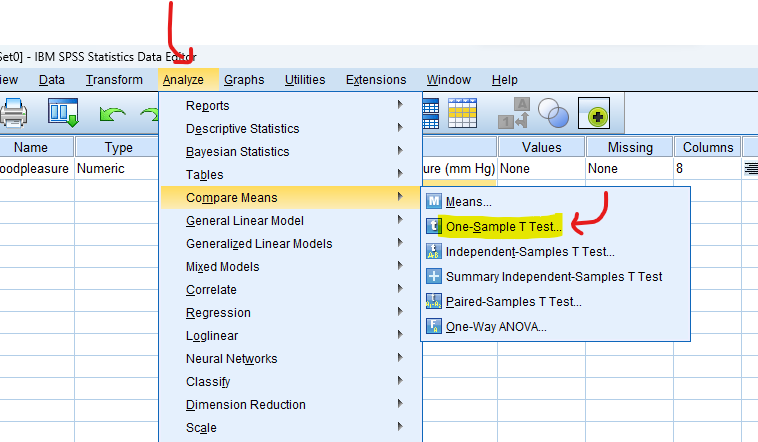
2. STEP: Access the Analyze Menu

In the top menu, locate and click on “Analyze.” Within the “Analyze” menu, navigate to “Compare Means” and choose ” One-Sample T Test.” Analyze > Compare Means> One-Sample T Test

3. STEP: Specify Variables 

In the dialogue box, choose the variable of interest Place one variable in the “Test Variables” box and specify the “test value” (population mean) against which you want to compare your sample mean.

4. STEP: Generate SPSS Output

Once you have specified your variables and chosen options, click the “OK” button to perform the analysis. SPSS will generate a comprehensive output, including the requested frequency table and chart for your dataset.

Note: Conducting One Sample T test in SPSS provides a robust foundation for understanding the key features of your data. Always ensure that you consult the documentation corresponding to your SPSS version, as steps might slightly differ based on the software version in use. This guide is tailored for SPSS version 25, and for any variations, it’s recommended to refer to the software’s documentation for accurate and updated instructions.

How to Interpret SPSS Output of One Sample T Test

SPSS will generate output, including descriptive statistics, the t-test value, degrees of freedom, and the p-value.

1. Descriptive Statistics:

   • Mean: Represents the average value of the sample.
   • Standard Deviation: Indicates the degree of variability or dispersion in the sample.
   • Standard Error: An estimate of the standard deviation of the sample mean.

2. One-Sample Test:

• t-Value: The t-statistic measures the difference between the sample mean and the population mean in terms of standard errors.
• Degrees of Freedom (df): The number of values in the final calculation of a statistic that are free to vary.
• p-Value: The probability of obtaining a t-value as extreme as the one observed, assuming the null hypothesis is true. If the p-value is less than or equal to 0.05, you can reject the null hypothesis, indicating a statistically significant difference.
• Mean Difference: The difference between the sample mean and the hypothesized population mean.
• 95% Confidence Interval (CI) for Mean Difference: A range within which we are 95% confident that the true population mean difference lies. if it does not include zero, it supports the rejection of the null hypothesis.

Interpret the results by comparing the p-value to your chosen significance level (commonly set at 0.05). If the p-value is less than or equal to 0.05, you can reject the null hypothesis, indicating a statistically significant difference.

A comprehensive understanding of SPSS output is essential for drawing accurate conclusions from your One Sample t Test results. In the subsequent section, we will guide you on how to effectively report these findings following the guidelines of the American Psychological Association (APA).

How to Report Results of One Sample T Test in APA

Reporting the results of a One Sample t Test in accordance with APA guidelines ensures clarity and consistency in scientific communication. Begin with a concise description of the analysis conducted, including the test name, sample size, and the variable under investigation.

For example, “A One Sample t Test was conducted to examine whether the mean [variable name] in a sample of [sample size] is significantly different from [population mean].”

Present the key statistical findings, including the t-test value, degrees of freedom, and p-value. For instance, “The results revealed a significant difference between the sample mean and the hypothesised population mean, t(df) = [t-test value], p = [p-value].”

Provide additional information such as effect size (e.g., Cohen’s d) and a confidence interval for the mean difference to offer a comprehensive overview of the results.

Get Help For Your SPSS Analysis

Embark on a seamless research journey with SPSSAnalysis.com, where our dedicated team provides expert data analysis assistance for students, academicians, and individuals. We ensure your research is elevated with precision. Explore our pages;

• SPSS Data Analysis Help – SPSS Helper,
• Quantitative Analysis Help,
• Qualitative Analysis Help,
• SPSS Dissertation Analysis Help,
• Dissertation Statistics Help,
• Statistical Analysis Help,
• Medical Data Analysis Help.

Connect with us at SPSSAnalysis.com to empower your research endeavors and achieve impactful results. Get a Free Quote Today!