Kaplan-Meier Analysis in SPSS
Discover Kaplan-Meier Analysis in SPSS! Learn how to perform, understand SPSS output, and report results in APA style. Check out this simple, easy-to-follow guide below for a quick read!
Struggling with Survival Analysis in SPSS? We’re here to help. We offer comprehensive assistance to students, covering assignments, dissertations, research, and more. Request Quote Now!
1. Introduction
The Kaplan-Meier analysis is a widely used statistical method for estimating survival probabilities in the presence of censored data. Developed by Edward Kaplan and Paul Meier, it allows researchers to visualize and compare the probability of survival over time across different groups. Therefore, this method is especially useful in medical research to track patient survival rates, but it is also applicable in fields like engineering and social sciences.
The Kaplan-Meier approach generates a survival curve, which represents the estimated probability of surviving past certain time points. It accounts for subjects who do not experience the event of interest during the study period by considering them as censored cases. Finally, This analysis provides an intuitive and effective way to study time-to-event data.
Time-To-Event (TTE) Data Analysis
Time-to-event (TTE) data analysis, also known as survival analysis, focuses on the time duration until a particular event of interest occurs. In medical research, this event is often death, relapse, or recovery, while in other fields, it could involve equipment failure, customer churn, or time to purchase. In addition, TTE data is unique because it allows researchers to account for both completed events and censored data, where the event has not yet occurred or the subject leaves the study before the event happens.
TTE data analysis is crucial because it enables researchers to estimate the probability of an event occurring at different times and to compare survival times across different groups. The analysis incorporates statistical models like the Kaplan-Meier estimator and Cox proportional hazards model to handle censored data and multiple covariates. Lastly, This makes TTE analysis a powerful tool for answering questions about treatment effectiveness, risk factors, and overall survival outcomes in a given population.
2. What is Kaplan-Meier Analysis in Statistics?
The Kaplan-Meier analysis, also known as the product-limit method, is a non-parametric statistic used to estimate the survival function from time-to-event data. The method calculates the probability of surviving for a specified time after treatment or intervention, while accounting for censored data.
In Kaplan-Meier analysis, each time an event occurs (such as death or equipment failure), the probability of survival is recalculated. The cumulative probability of survival is then obtained by multiplying the probabilities of survival up to that time point. This allows researchers to track survival rates over time and make comparisons between different groups.
3. What is Kaplan-Meier Analysis used for?
We use Kaplan-Meier analysis in medical and clinical research to estimate the survival times of patients and compare different treatment groups. Researchers apply this analysis to evaluate the effectiveness of new treatments, track disease progression, or estimate the time until an event such as death or relapse.
Beyond healthcare, Kaplan-Meier analysis is useful in engineering for assessing the reliability and failure rates of machinery and equipment. It can also be applied in marketing to measure customer retention rates or the time until customers discontinue a service. Its versatility makes it a go-to method for time-to-event studies across various fields.
4. Explaining the Differences Between Survival Analysis, Kaplan-Meier, Cox Regression, and ROC Curve
- Survival Analysis:
- A statistical method used to analyse the time until an event occurs, particularly in medical, engineering, and social sciences.
- Includes several techniques to handle censored data and compare survival times between groups.
- Kaplan-Meier:
- A non-parametric method that estimates survival probabilities over time.
- It produces a survival curve and is useful for visualising the probability of survival at different time points.
- Commonly used to compare survival between two or more groups.
- Cox Regression (Proportional Hazards Model):
- A semi-parametric model used to assess the effect of several covariates on survival time.
- It estimates hazard ratios to determine how variables impact the risk of the event occurring.
- ROC Curve:
- A graphical plot used to assess the accuracy of diagnostic tests, focusing on sensitivity and specificity.
- Though not specifically for survival data, it can be used in survival analysis to identify optimal cut-off points for predictors.
5. What are the Assumptions of the Kaplan-Meier Analysis?
Before conducting survival analysis, it is crucial to meet certain assumptions to ensure accurate results. These assumptions are essential for models like Kaplan-Meier and Cox Regression. By understanding and verifying these assumptions, researchers can make sure their findings are valid and reliable. The Kaplan-Meier analysis rests on the following assumptions:
- Researchers must clearly define and consistently measure the event of interest.
- Censored cases should share the same future risk as those who experience the event.
- Each individual’s event must occur independently, without influencing others.
- The timing of censoring should not relate to the likelihood of the event occurring (non-informative censoring).
- Subjects lost to follow-up should not introduce bias into the analysis
6. What is the Hypothesis of the Kaplan-Meier Analysis?
In Kaplan-Meier analysis, the null hypothesis typically states that there is no difference in survival between the groups being compared. For example, in clinical trials, the null hypothesis would claim that the survival probabilities for patients receiving two different treatments are equal over time.
The alternative hypothesis suggests that there is a difference in survival between the groups. By testing this hypothesis, researchers can determine whether the treatment or intervention has a statistically significant impact on survival outcomes.
7. An Example of the Kaplan-Meier Analysis
Let’s consider a clinical study where researchers want to compare the survival rates of patients receiving a new treatment versus a standard treatment. The main variables involved are time to event, which measures the duration (in months) until the event (e.g., death or relapse) occurs, and event, which is coded as 1 if the event occurred and 0 if the patient was censored (i.e., the event did not occur during the study). Additionally, the patients are divided into two groups: those receiving the new treatment (coded as 1) and those receiving the standard treatment (coded as 0).
The Key variables:
- Time-to-Event Variable: This represents the time in months until the event occurs (e.g., death, relapse) or until the study ends (if censored).
- Event Variable: The event is coded as 1 if the event occurred (e.g., the patient experienced death or relapse) and 0 if the patient is censored (e.g., the event didn’t happen during the study).
- Treatment Group Variable: This categorical variable indicates whether the patient received the new treatment (coded as 1) or the standard treatment (coded as 0).
For this example, researchers use Kaplan-Meier survival analysis to estimate and compare the survival probabilities over time between the two treatment groups. The Kaplan-Meier method allows the estimation of survival functions even when some data points are censored, making it an ideal tool for this type of study. In this scenario, the researchers are particularly interested in determining whether the new treatment significantly improves the patients’ chances of survival compared to the standard treatment.
Step by Step: Running Kaplan-Meier Analysis in SPSS Statistics
Let’s embark on a step-by-step guide on performing the Kaplan-Meier Analysis using SPSS
- STEP: Load Data into SPSS
Commence by launching SPSS and loading your dataset, which should encompass the variables of interest – a categorical independent variable. If your data is not already in SPSS format, you can import it by navigating to File > Open > Data and selecting your data file.
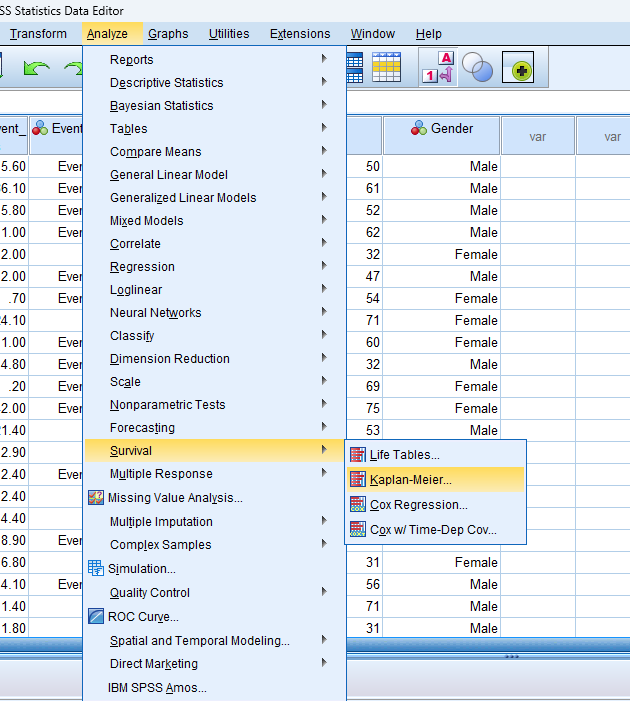
- STEP: Access the Analyze Menu
In the top menu, Go to ‘Analyse’ > ‘Survival’ > select either ‘Kaplan-Meier’ or ‘Cox Regression’ based on your objective.
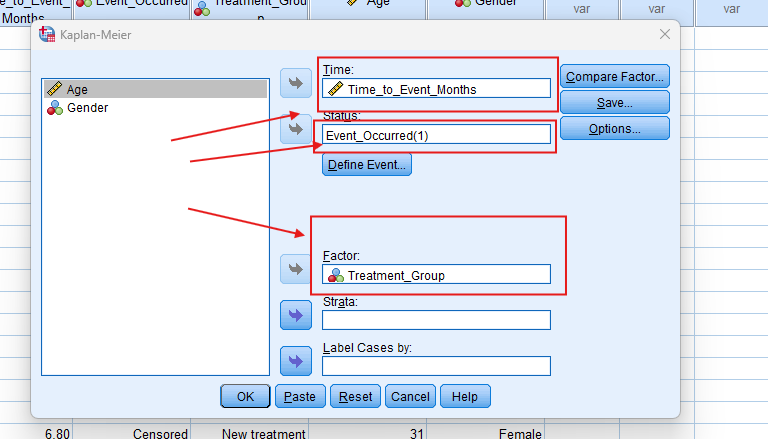
- STEP: Specify Variables
- For Kaplan-Meier, select the time and event variables, and include any grouping variable (e.g., treatment group).
- For Cox Regression, specify time, event, and covariates to be included in the model.
- STEP: Generate SPSS Output
- Click ‘OK’ after selecting your variables and method. SPSS will run the analysis and generate output tables and survival curves.
Note: Conducting Kaplan-Meier Analysis in SPSS provides a robust foundation for understanding the key features of your data. Always ensure that you consult the documentation corresponding to your SPSS version, as steps might slightly differ based on the software version in use. This guide is tailored for SPSS version 25, and for any variations, it’s recommended to refer to the software’s documentation for accurate and updated instructions.
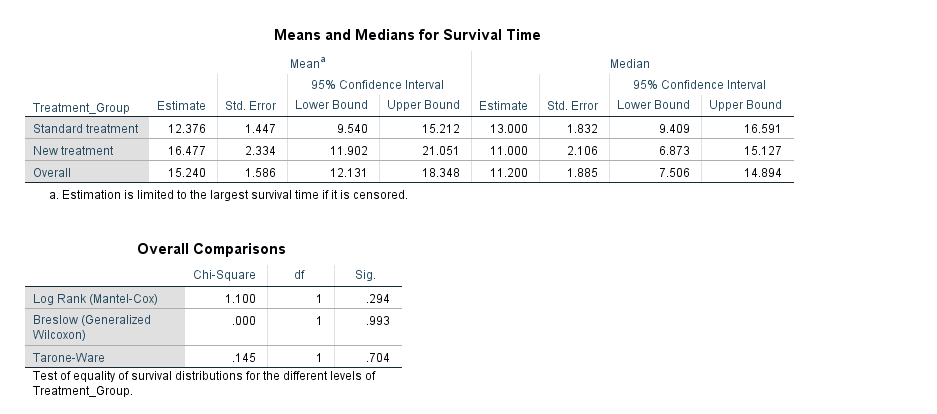
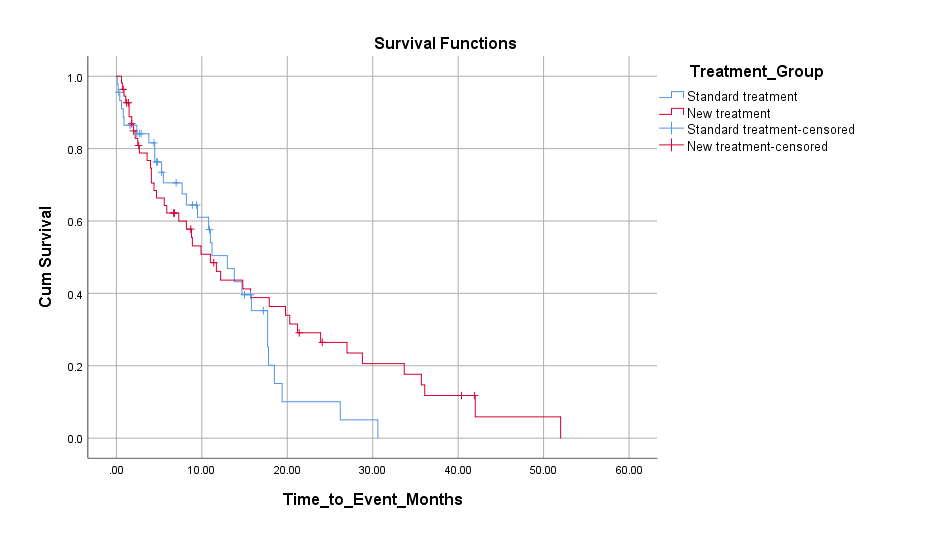
SPSS Output for Kaplan-Meier Analysis
9. How to Interpret SPSS Output of Kaplan-Meier Analysis
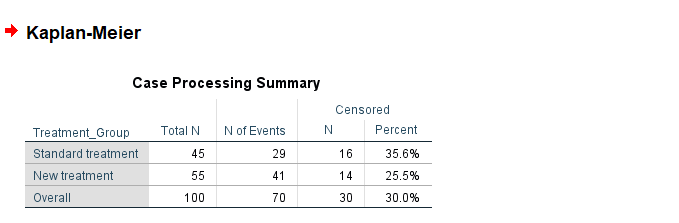
SPSS will generate output, including Case Processing Summary, Survival Table, Means and MEdian Survival Time, Overall comparison and Survival Function Plot
- Kaplan-Meier Output:
- Survival Table/Life Table: Shows the number of events and censored cases at each time point.
- Survival Function Plot: Provides the estimated survival probability over time. Look at the steep drops to see where the highest event rates occur.
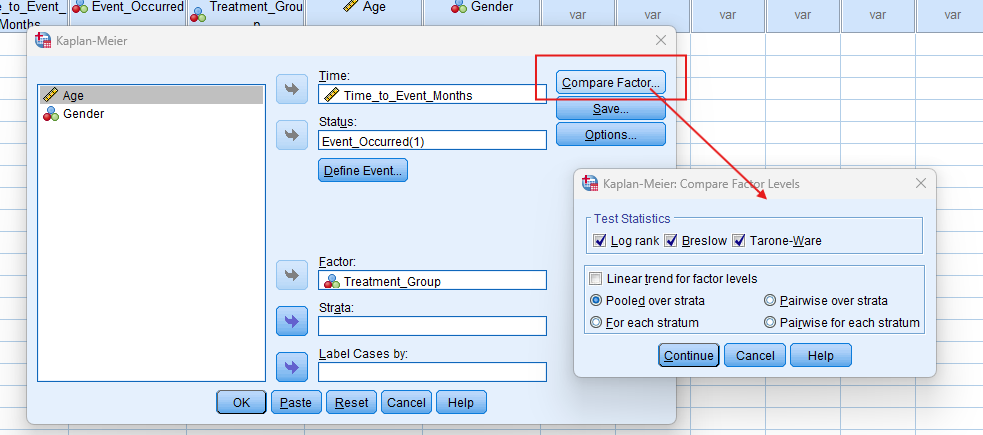
- Log-Rank Test Table: Compares survival curves between groups and provides a p-value to determine significance. If p < 0.05, there is a significant difference between groups.
- Cox Regression Output:
- Model Summary: Reports the overall model fit, including -2 Log Likelihood, AIC, and BIC.
- Covariate Table: Displays hazard ratios (HR) for each covariate, with confidence intervals. An HR > 1 means increased risk, while HR < 1 means reduced risk.
- Proportional Hazards Test: Confirms whether the proportional hazards assumption holds (important for valid results).
10. How to Report Results of Kaplan-Meier Analysis in APA
Reporting the results of Kaplan meier analysis in APA (American Psychological Association) format requires a structured presentation. Here’s a step-by-step guide in list format:
- Introduction: Briefly describe the purpose of the analysis and the theoretical background.
- Method: Detail the data collection process, variables used, and the model specified.
- Results: Present the parameter estimates with their standard errors, and significance levels.
- Figures and Tables: Include relevant plots and tables, ensuring they are properly labelled and referenced.
- Discussion: Interpret the results, highlighting the significance of the findings and their implications.
- Conclusion: Summarise the main points and suggest potential areas for further research.

Get Support For Your SPSS Data Analysis
Embark on a seamless research journey with SPSSAnalysis.com, where our dedicated team provides expert data analysis assistance for students, academicians, and individuals. We ensure your research is elevated with precision. Explore our pages;
- Biostatistical Modeling Expert
- Statistical Methods for Clinical Studies
- Epidemiological Data Analysis
- Biostatistical Support for Researchers
- Clinical Research Data Analysis
- Medical Data Analysis Expert
- Biostatistics Consulting
- Healthcare Data Statistics Consultant
- SPSS Help by Subjects Area: Psychology, Sociology, Nursing, Education, Medical, Healthcare, Epidemiology, Marketing
Connect with us at SPSSAnalysis.com to empower your research endeavors and achieve impactful data analysis results. Get a FREE Quote Today!