Kendall's Tau Correlation in SPSS

Introduction

Embarking on the statistical journey of understanding relationships between variables leads us to the realm of Kendall’s Tau Correlation, a powerful tool in the world of data analysis. This post aims to demystify Kendall’s Tau Correlation in SPSS, providing insights into its applications and the nuanced way it assesses the strength and direction of associations between variables. Whether you’re navigating the intricate landscape of statistical analyses or seeking a robust alternative to parametric measures,

Kendall’s Tau Correlation offers a non-parametric solution for scenarios where the assumptions of other methods may not be met. As we delve into the intricacies of Kendall’s Tau, we’ll uncover its inner workings, explore its assumptions, and guide you through a practical example in SPSS.

What are the 5 Correlation Analyses?

Correlation Analysis offers various methods to explore associations between variables. Besides the commonly used Pearson Correlation, others include Spearman’s Rho rank order, Kendall’s Tau, Partial Correlation, and Canonical Correlation.

1. Pearson Correlation Analysis

• Description: Measures the linear relationship between two continuous variables.
• Applicability: Best suited for variables with a linear association and normally distributed data.
• Range: Correlation coefficient (r) ranges from -1 to 1.
• Interpretation: Positive values indicate a positive linear relationship, negative values indicate a negative linear relationship, and 0 implies no linear relationship.

2. Spearman Rank-Order Correlation

• Description: Non-parametric measure assessing the monotonic relationship between two variables.
• Applicability: Suitable for ordinal data or when assumptions of normality are violated.
• Procedure: Converts data into ranks and compute the correlation based on the rank differences.
• Interpretation: The correlation coefficient (rho) ranges from -1 to 1, with a similar interpretation to Pearson.

3. Kendall’s Tau

• Description: Non-parametric measure assessing the strength and direction of a monotonic relationship.
• Applicability: Similar to Spearman, suitable for ordinal data and non-normally distributed data.
• Procedure: Measures the number of concordant and discordant pairs in the data.
• Interpretation: Kendall’s Tau (τ) ranges from -1 to 1, with 0 indicating no association and values towards -1 or 1 indicating stronger associations.

4. Partial Correlation

• Description: Examines the relationship between two variables while controlling for the influence of one or more additional variables.
• Applicability: Useful when there is a need to isolate the direct relationship between two variables.
• Procedure: Calculates the correlation between two variables after removing the shared variance with the control variable(s).
• Interpretation: Provides insights into the unique contribution of each variable to the correlation.

5. Canonical Correlation

• Description: Assesses the association between two sets of variables.
• Applicability: Useful when dealing with multiple sets of variables simultaneously.
• Procedure: Maximizes the correlation between linear combinations of variables from each set.
• Interpretation: Provides information on the overall relationship between sets of variables, producing canonical correlation coefficients.

Understanding the characteristics and applications of each correlation analysis method equips researchers with a versatile toolkit for exploring diverse data scenarios.

Kendall’s Tau Correlation

Kendall’s Tau Correlation, named after the British statistician Maurice Kendall, stands as a non-parametric measure that quantifies the strength and direction of the association between two variables. Unlike Pearson correlation, Kendall’s Tau doesn’t rely on the assumption of linearity, making it particularly useful for ordinal or ranked data. The correlation coefficient generated by Kendall’s Tau is based on the concordant and discordant pairs of observations, providing a robust measure of association even when dealing with non-normally distributed data. As we progress, we’ll uncover the essence of Kendall’s Rank Correlation Coefficient, unravel its assumptions, and delve into the hypotheses it seeks to address in statistical analyses.

Kendall’s Rank Correlation Coefficient

At the core of Kendall’s Tau Correlation lies the rank correlation coefficient, a numerical measure reflecting the degree of agreement between the orderings of the variables. The coefficient is derived from assessing the number of concordant pairs (where the order is preserved) and discordant pairs (where the order is reversed) in the data.

Kendall’s Tau takes values between -1 and 1, where -1 indicates perfect inverse agreement, 1 signifies perfect agreement, and 0 suggests no monotonic relationship. This makes it a versatile measure for variables with ordinal properties or those not adhering strictly to linear patterns. In essence, Kendall’s Tau provides a robust method for capturing the underlying associations between variables in a way that transcends the limitations of parametric assumptions.

Assumption of Kendall’s Tau Correlation Analysis

To ensure the reliability of Kendall’s Tau Correlation Analysis in SPSS, it’s essential to be aware of its underlying assumptions:

• Independence: The observations should be independent of each other for meaningful correlation assessment.
• Random Sampling: The data should be obtained through a random sampling process, contributing to the generalizability of the results.
• No Ties in Data: Tied ranks in the data, where two or more observations share the same value, may require adjustments in the correlation coefficient calculation.

Adhering to these assumptions ensures the validity of Kendall’s Tau in uncovering meaningful relationships between variables. As we proceed, we’ll explore the hypotheses that Kendall’s Tau addresses, providing a comprehensive understanding of its applications in statistical analyses.

Hypothesis of Kendall’s Tau Correlation Analysis

Kendall’s Tau Correlation Analysis allows researchers to test specific hypotheses regarding the relationships between variables. The hypotheses include both the null hypothesis (H0) and the alternative hypothesis (H1):

• Null Hypothesis: There is no significant monotonic association between the variables.
• Alternative Hypothesis: There is a significant monotonic association between the variables.

Understanding and formulating these hypotheses is pivotal for conducting meaningful Kendall’s Tau Correlation Analysis, guiding researchers in interpreting the statistical results in the context of the specific relationship they aim to explore.

 Example of Kendall’s Tau Correlation

Let’s consider a practical example involving the assessment of job satisfaction and work performance among employees in a company. Each employee is ranked based on their job satisfaction level and work performance, both on a scale from 1 to 10. The goal is to explore whether there is a monotonic association between job satisfaction and work performance ranks.

• Null Hypothesis (H0): There is no significant monotonic association between job satisfaction and work performance ranks.
• Alternative Hypothesis (H1): There is a significant monotonic association between job satisfaction and work performance ranks.

This example enables us to practically apply Kendall’s Tau Correlation to assess whether employees who are more satisfied with their jobs tend to have higher ranks in work performance, or vice versa.

Conducting Kendall’s Tau Correlation Analysis on such data will provide insights into the strength and direction of the monotonic association between these two variables. As we proceed, we’ll guide you through the step-by-step process of performing Kendall’s Tau Correlation Analysis in SPSS, ensuring a clear and practical understanding of its application.

Step by Step: Running Kendall’s Tau Correlation in SPSS Statistics

Now, let’s delve into the step-by-step process of conducting Kendall’s Tau Correlation using SPSS.  Here’s a step-by-step guide on how to perform a Kendall’s Rank Correlation Analysis in SPSS:

1. STEP: Load Data into SPSS

Commence by launching SPSS and loading your dataset, which should encompass the variables of interest – a categorical independent variable. If your data is not already in SPSS format, you can import it by navigating to File > Open > Data and selecting your data file.

2. STEP: Access the Analyze Menu

In the top menu, locate and click on “Analyze.” Within the “Analyze” menu, navigate to “Correlate” and choose ” Bivariate” Analyze > Correlate> Bivariate

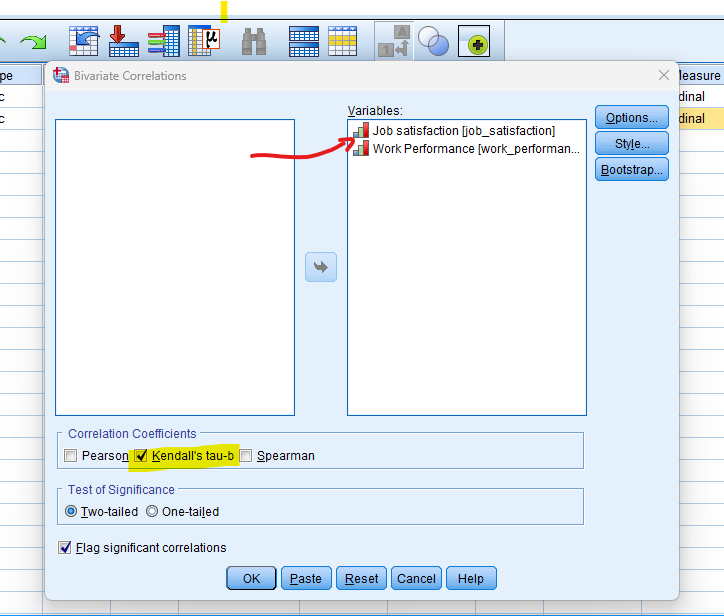
3. STEP: Choose Variables

– In the “Bivariate Correlations” dialogue box, select the variables you want to analyze. Move the variables of interest from the list of available variables to the “Variables” box.

– Check Kendall for the Correlation Coefficient.

4. STEP: Generate SPSS Output

Once you have specified your variables and chosen options, click the “OK” button to perform the analysis. SPSS will generate a comprehensive output, including the requested frequency table and chart for your dataset.

Executing these steps initiates the Kendall Rank Correlation Analysis in SPSS, allowing researchers to assess the impact of the teaching method on students’ test scores while considering the repeated measures. In the next section, we will delve into the interpretation of SPSS output for Kendall’s Tau Correlation Analysis.

Note

Conducting a Kendall Rank Correlation Analysis in SPSS provides a robust foundation for understanding the key features of your data. Always ensure that you consult the documentation corresponding to your SPSS version, as steps might slightly differ based on the software version in use. This guide is tailored for SPSS version 25, and any variations, it’s recommended to refer to the software’s documentation for accurate and updated instructions.

How to Interpret SPSS Output of Kendall’s Tau Correlation

Interpreting the SPSS output of Kendall’s Tau Correlation Analysis involves examining the correlation matrix and associated statistics. The correlation matrix displays the correlation coefficients (r) between pairs of variables. Each cell in the matrix corresponds to the correlation between two variables, and the diagonal contains the correlation of each variable with itself, which is always 1. The correlation coefficient ranges from -1 to 1, with values closer to 1 or -1 indicating a stronger linear relationship.

Key elements to interpret in the output include:

• Correlation Coefficient (tau_b): The strength and direction of the linear relationship.
• Significance (p-value): Indicates whether the observed correlation is statistically significant.
• Sample Size (N): The number of data points used in the analysis.

How to Report Results of Kendall’s Tau Correlation Analysis in APA

Reporting results in APA format involves providing key information such as the correlation coefficient (r), degrees of freedom, significance level, and sample size. For instance:

• Introduction: Begin by introducing the analysis, mentioning that a Kendall’s Tau correlation analysis was conducted to examine the relationships between the specified variables.
• Correlation Coefficients: Report the Kendall’s Tau correlation coefficients (tau_b) for each pair of variables. Clearly state which variables were analysed and provide the numerical values.
• Significance Levels: Indicate the significance levels (p-values) associated with each correlation coefficient. This helps determine whether the observed correlations are statistically significant.
• Interpretation: Interpret the strength and direction of each correlation coefficient. Use terms such as “strong,” “moderate,” or “weak” to describe the magnitude of the relationship.
• Descriptive Statistics (Optional): Present descriptive statistics for each variable, including means, standard deviations, and sample sizes. This provides context for the correlation results.
• Confidence Intervals (Optional): If confidence intervals were calculated, report them to provide a range of values within which the true population correlation is likely to fall.
• Limitations (Optional): Acknowledge any limitations of the analysis, such as potential confounding variables or the cross-sectional nature of the data.

Get Help For Your SPSS Analysis

Embark on a seamless research journey with SPSSAnalysis.com, where our dedicated team provides expert data analysis assistance for students, academicians, and individuals. We ensure your research is elevated with precision. Explore our pages;

• SPSS Data Analysis Help – SPSS Helper,
• Quantitative Analysis Help,
• Qualitative Analysis Help,
• SPSS Dissertation Analysis Help,
• Dissertation Statistics Help,
• Statistical Analysis Help,
• Medical Data Analysis Help.

Connect with us at SPSSAnalysis.com to empower your research endeavors and achieve impactful results. Get a Free Quote Today!